本文探讨了中奖概率与数学期望的关系及其在实际中的应用，旨在帮助读者理解概率与期望值在实际决策中的重要性。通过几个实际例子，分析了中奖概率对期望值的影响，并介绍了如何利用数学期望进行优化决策。本篇文章不仅适用于彩票等博彩类应用，还涉及到投资决策等领域。

1、中奖概率的基本概念

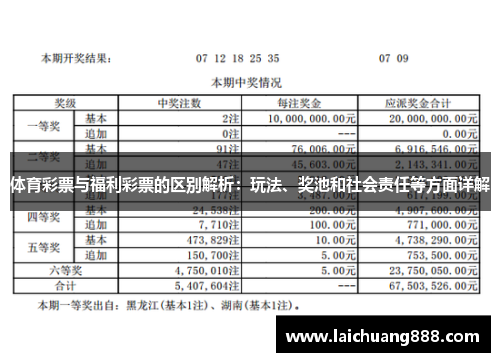
中奖概率是指在某个随机事件中，发生中奖结果的可能性大小。在彩票、抽奖等随机游戏中，中奖概率是决定是否值得参与的重要因素。通常情况下，中奖概率的计算基于事件发生的总可能性数和中奖的可能性数。举例来说，在一场有1000个奖项的抽奖活动中，若参与者总数为10000人，那么中奖概率就是1/10。

在不同的游戏中，中奖概率往往是根据游戏规则设定的。例如，某些彩票的中奖概率可能非常低，常见的概率为百万分之一甚至更小。了解这些概率，对于参与者来说非常重要，因为它直接影响到他们的期望收益和决策。

从数学角度看，中奖概率是一个重要的统计量，它不仅体现了随机事件发生的可能性，也为后续计算数学期望提供了基础数据。理解中奖概率对于分析和优化决策具有重要意义。

2、数学期望的定义与计算

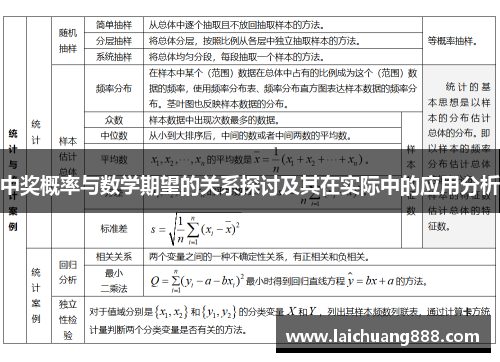
数学期望，又称期望值或均值，是随机变量可能取值的加权平均数。它可以看作是长期实验中随机变量的平均结果。期望值的计算公式为每个可能结果的数值乘以其发生的概率，所有结果相加。具体公式为E(X) = Σ [x_i * P(x_i)]，其中x_i是随机变量可能的值，P(x_i)是该值的概率。

在彩票和抽奖等场景中，数学期望用于评估参与某个游戏是否值得。假设某彩票的价格为10元，奖池总金额为100万元，而中奖概率为1/1000000，那么我们可以通过计算期望值来判断是否参与。这种期望值不仅能够帮助玩家评估投入的价值，还能反映出参与这种活动可能的平均收益。

数学期望在投资决策、风险评估等领域同样具有重要应用。通过对不同选项的期望值进行比较，投资者可以选择最优的投资策略。同样，在保险、贷款等金融活动中，期望值的计算也是判断风险和回报的基础。

3、中奖概率与数学期望的关系

中奖概率与数学期望之间存在密切关系。中奖概率是影响数学期望的一个关键因素，中奖概率越高，数学期望值通常也越高。反之，若中奖概率很低，虽然中奖金额很大，但数学期望可能依然较低，甚至为负数。因此，中奖概率决定了期望收益的大小。

举一个简单的例子：如果某彩票的价格为10元，奖池金额为100万元，中奖概率为1/1000000，那么数学期望值为：10元 × 1/1000000 = 0.00001元。这意味着，从数学期望的角度看，参与此彩票的期望收益几乎为零。如果中奖概率提高到1/10000，期望值就会大幅上升。

在实际应用中，我们可以通过调整概率、奖池金额以及彩票价格等因素，优化数学期望。对于博彩公司或彩票主办方来说，设定合理的概率和奖池金额是保证盈利的关键；而对于玩家来说，理解这些关系能够帮助他们做出更理性的决策。

4、中奖概率与数学期望的实际应用

中奖概率与数学期望的概念不仅局限于彩票等娱乐活动，还广泛应用于投资、金融等领域。在投资领域中，投资者会根据不同资产的回报率和风险概率，计算期望收益，以此来选择最有利的投资组合。举例来说，股市中的某些股票虽然回报潜力巨大，但由于风险较高，其数学期望可能并不如稳健型基金。

在金融衍生品如期权、期货交易中，数学期望的计算也是投资者决策的依据之一。通过对不同市场条件下的概率进行分析，投资者可以选择最优的交易策略。在此类高风险、高回报的环境下，参与者需要深刻理解中奖概率与数学期望的关系，才能合理规避风险并优化收益。

此外，保险行业也运用数学期望来设定保费与赔付比例。在设计保险产品时，保险公司会根据理赔概率计算期望值，并据此决定保费金额。保险公司在调整保费与赔付比例时，实际上是在做一个期望值的平衡，既要保证盈利，又要确保客户的满意度。

总结：

中奖概率与数学期望的关系是概率论与决策理论中的重要内容。通过理解概率和期望的基本概念，参与者能够更加理性地评估和选择参与各种活动或投资的风险与回报。在彩票等博彩活动中，数学期望帮助参与者判断是否值得投入；而在金融、投资等行业，期望值的计算更是决策和风险管理的基础。

通过对概率与期望关系的深入分析，我们可以看到，它们不仅仅是数学的抽象概念，而是实际生活中不可忽视的决策工具。无论是在娱乐、投资，还是在日常的决策过程中，理解并应用中奖概率与数学期望的关系，能够帮助我们做出更加明智的选择，实现最优的决策效果。